基本概念
在一张图 \(G=(V,E)\) 中,能够连接 \(G\) 中所有结点的树,称之为生成树,又因为每条边都具有权重,所以称所有生成树中权重之和最小的为 最小生成树(Minimum Spanning Tree)。
在本文中讨论的两种算法均采用贪心政策,如果将最小生成树中的边当成一个集合,那么在每一步中两个算法都会挑选一条边加入这个集合中,这样的边称之为 安全边 。
Kruskal 算法
Kruskal 算法中先用一个不相交集将每一个结点都当作一棵树的结点,而寻找安全边的策略则是每次都挑选一个权重最小的边,每一次加入就可以将两棵树合并,直至所有结点都被加入,此时生成的树即为最小生成树。
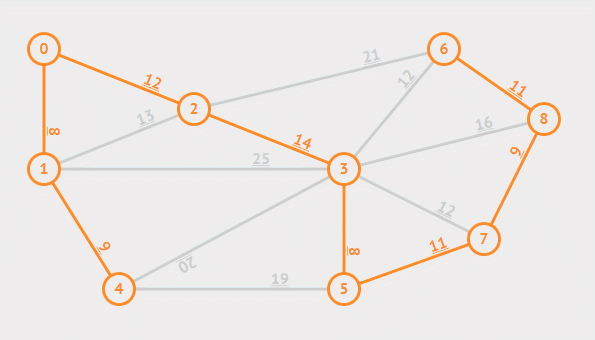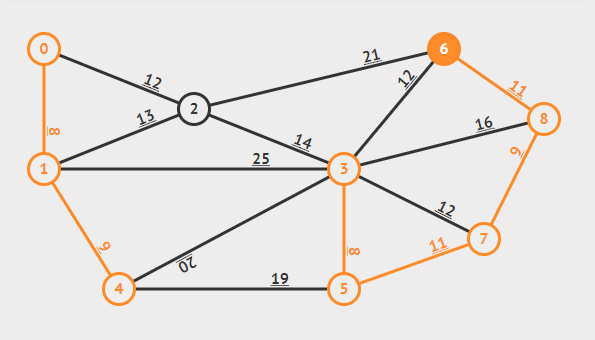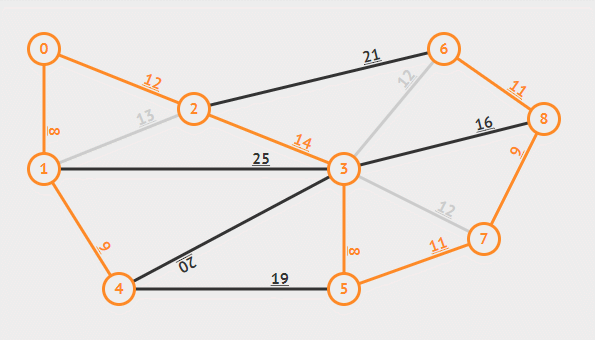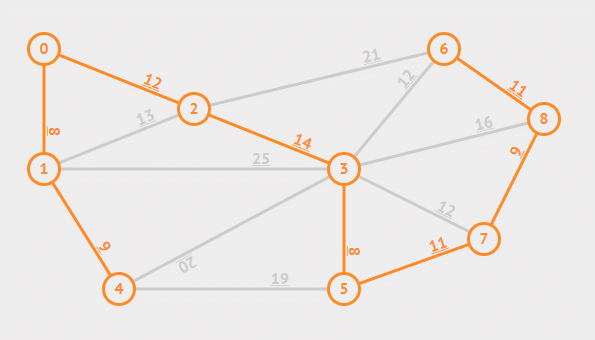
然而当加入了一定多的边后,就需要决定是否将这条边加入集合中,判断的策略是边的两个结点是否属于同一颗树,因为如果已经属于同一棵树说明他们已经连通,不再需要新的边,而如果不属于同一棵树,那么这条边是能够将两棵树合并的权重最小的边,具体证明在此不赘述。
如下为 Kruskal 算法的示例代码。
1
2
3
4
5
6
7
8
9
10
11
12
void MST_Kruskal()
{
DisjointSet<Vertex> Set(G) //将所有结点放入不相交集中并互相独立
priority_queue<Edge> H(G.E) //用一个优先队列来保证边的权重从小到大
while (!H.empty()) {
Edge E = H.pop();
if (Set.Find(E.v1) != Set.Find(E.v2)) { //判断两个结点是否处于同一颗树中
Set.Union(E.v1, E.v2);
}
}
}
Java实现供参考
Prim 算法
Prim 算法可以从任意一个结点开始,然后逐步长大直至所有的结点都被纳入集合 A 中。每一次挑选安全边的策略是总是挑选集合 A 中结点向外延伸的边中权重最小的那条。
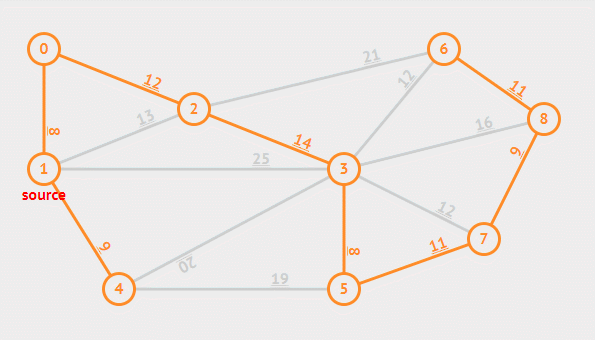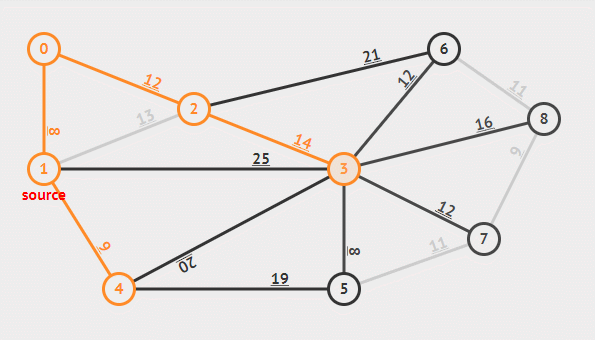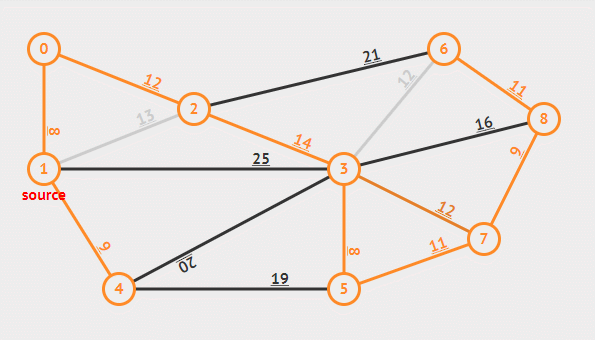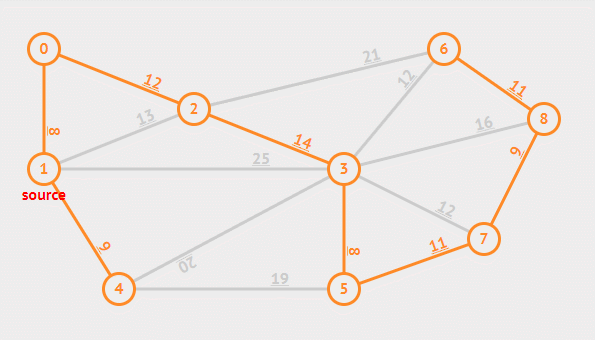
有时会遇到最小的边两侧的结点已经被加入集合中,此时应将这条边舍去,因为最小生成树不能够成环。
实际实现中用一个优先队列来更快速的得到一条新的边,每个结点都赋予一个 key 和 parent 属性来保存与当前结点中连接最小的权重和前一个结点。伪代码如下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void MST_Prim(Vertex V) {
for (Vertex v in G.V) { //将所有结点初始化
v.key = INF;
v.parent = null;
}
V.key = 0;
priority_queue<Vertex> Q(G.V); //以key为属性维护优先队列,并将所有的结点放入
while (!Q.empty()) {
Vertex u = Q.pop();
for (Vertex v in u.adj) { //遍历所有与 u 相连结点
if (v in Q && w(u, v) < v.key) { //如果存在边且权重小
v.parent = u
v.key = w(u, v)
}
}
}
}
Java实现供参考
总结
两个方法每次都是找最小的边加入到结果中。 Kruskal 算法每次挑选所有边中权重最小的,Prim 算法每次找与现有结点相连边中权重最小的。每次加入的时候 Kruskal 需要判断这条边是否需要,即两个结点是否已经在树中,而 Prim 算法则只需要找到权中最小的即可。
两个方法效率基本相同,一般实现下时间复杂度均为 \(O(E lgV)\),但 Prim 算法利用斐波那契堆还可进一步优化到 \(O(E + VlgV)\)。相对来说, Kruskal 更适合邻接矩阵,Prim 更适合邻接链表。