heap 又称二叉堆,是一个十分常用的数据结构,可以看成一个完全二叉树,但可以使用数组来实现。在这有过更详细的介绍。
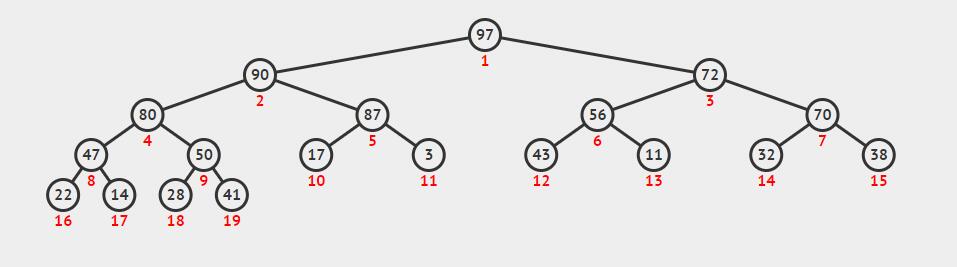
在 STL 中,heap 并不作为一个容器,而是在 algorithm 库中以算法的形式实现,并且都接受first和last两个参数,并要求其为 随机迭代器(Random Access Iterator)。另外,这些函数都提供两个版本,一个通过 < 来比较,从而实现最大堆,另一个利用模板,从而可以指定比较函数Comp来比较。两者实现相似,所以本文用前者,另一版本可以在Github查看。
标准中定义了如下五个函数:
is_heap: 判断 [first,last) 中元素是否为最大堆。make_heap:在 [first,last) 中构造最大堆。push_heap:将last-1中元素插入到 [first,last-1) 的最大堆中。pop_heap:交换在位置first的值和在位置last-1的值,并令子范围 [first,last-1) 变为最大堆。sort_heap:转换最大堆 [first,last) 为以升序排序的范围。
辅助函数
首先是用于得到子节点或者父节点的函数,使之后实现更为方便。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
template<class Distance>
Distance _left(Distance i) {
return 2 * i + 1;
}
template<class Distance>
Distance _right(Distance i) {
return 2 * i + 2;
}
template<class Distance>
Distance _parent(Distance i) {
return (i - 1) / 2 ;
}
另外还有个函数帮助维护堆的性质,使某个不满足堆性质的节点移动到正确的位置。思路很简单,就是和左右节点比较,在三个节点中找到最大的一个与其互换,然后对新子树再进行该操作。若无需说明已满足最大堆条件则结束。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
template<class RandomIt,class Distance>
void _max_heapify(RandomIt first,Distance index,Distance size) {
Distance l = _left(index),r=_right(index);
Distance largest;
if(l<size&&*(first+l)>*(first+index)) {
largest = l;
} else {
largest = index;
}
if(r<size&&*(first+r)>*(first+largest)) {
largest = r;
}
if(largest!=index) {
auto tmp = *(first + index);
*(first + index) = *(first + largest);
*(first + largest) = tmp;
_max_heapify(first, largest, size);
}
}
前一个函数使得节点可以下降,同时很可能需要将某个节点上升,思路与前者相似。
1
2
3
4
5
6
7
8
9
10
11
template<class RandomIt,class Distance>
void _percolate_up(RandomIt first,Distance index) {
auto value = *(first + index);
auto parent =_parent(index);
while (index!=0&& value > *(first + parent)) {
*(first + index) = *(first + parent);
index = parent;
parent = _parent(parent);
}
*(first + index) = value;
}
push_heap
这一函数用于将最后一个元素插入到前面的最大堆中,所以我们只需要利用percolate_up将最后一个元素上升即可。
1
2
3
4
template<class RandomIt>
void push_heap(RandomIt first,RandomIt last) {
_percolate_up(first, last - first-1);
}
pop_heap
pop_heap用于将最大的元素出堆,但实际上是将其放到最后,而原本在最后的元素需要将其调整到合适的位置。所以这一函数思路为将最前和最后的元素互换,再对新的第一个元素调用max_heapify维护堆的性质。
1
2
3
4
5
6
7
template<class RandomIt>
void pop_heap(RandomIt first, RandomIt last) {
auto tmp = *first;
*first= *(last - 1);
*(last - 1) = tmp;
_max_heapify(first, first-first, last - first-1);
}
make_heap
max_heapify可以使某个节点满足堆性质,那么对所有节点都调用一次就可以得到最大堆。而有一半节点为叶节点,所以只用对一半节点做该操作。
1
2
3
4
5
6
7
template<class RandomIt>
void make_heap(RandomIt first, RandomIt last) {
auto size = last - first;
for(auto i=size/2;i>=0;--i) {
_max_heapify(first, i, size);
}
}
sort_heap
利用pop_heap将最大的元素放至最后这一特性,那么只需要将所有元素出堆就得到了有序的数组。
1
2
3
4
5
6
template<class RandomIt>
void sort_heap(RandomIt first,RandomIt last) {
while(last-first>1) {
lix::pop_heap(first, last--);
}
}
is_heap
依次遍历并判断是否满足最大堆性质便可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
template<class RandomIt,class Distance>
bool _is_heap(RandomIt first,Distance size){
for(Distance i=0;i<size/2;++i) {
if (_left(i) < size&&*(first + i) < *(first + _left(i)))
return false;
if (_right(i) < size&& *(first + i) < *(first + _right(i)))
return false;
}
return true;
}
template< class RandomIt >
bool is_heap(RandomIt first, RandomIt last) {
return _is_heap(first, last - first);
}
后记
本文中的实现主要依靠_max_heapify和_percolate_up两个函数。另外还有个 SGI_STL 的实现有所差异。这些关于堆的函数在优先队列的实现中有极大帮助。